候选边集

解释

k-opt运算中，不可能遍历所有边进行k-opt交换计算(计算复杂度为指数型)
所以候选边集的目标，就是为每个节点预先筛选少数可能属于最优解的边
直接将复杂度降为Ο(1)

核心:α-nearness

思想:最优解的边通常与最小生成树(MST)或1-tree和Herd-kerp松弛结构中的边高度 相关
Step1.构建最小生成树
什么是最小生成树？
最小生成树就是权重之和最小的生成树
那什么又是生成树呢？
生成树就是对于具有n的点的连通图，遍历后包含所有的点并保持图连通
最后的结构一定是具有n-1条边的树，称为生成树
使用Prim或Kruskal算法构建完全图MST
为什么MST会和TSP相关?
因为MST是连接所有节点中最小总权重的树，所以TSP的最优解通常包含MST中的部分边
我们知道，TSP的最优解是一个哈密顿回路（即访问每个节点恰好一次）
而MST是权重之和最小的树
所以TSP权重之和≥MST权重之和
故MST为TSP提供了一个简单下界（可能的最优解）
可以用于评估算法性能，也为后续优化提供了一个好的起点
但非常多的时候，MST的权重之和远小于TSP的权重之和
所以需要采用另一些方式来计算更准确的下界

Step2.计算1-tree和Held-karp松弛
什么是1-tree？
1-tree其实是MST的变体
构造步骤如下:
1.选择一个节点
2.构造除该节点外的最小生成树
3.添加两条最短边，将该节点连接到树上，形成包含所有节点的单一回路
此时1-tree的权重是在以下条件下最小的:
1.包含所有节点
2.形成一个树状结构（无回路）外加一个通过固定节点的回路
示例图如下

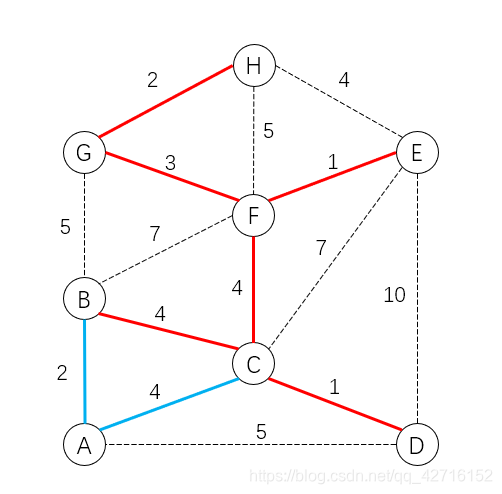
Held-karp松弛
思想:通过引入节点势调整边权重，使1-tree权重最小化同时迫使1-tree的结构逼近合法TSP回路（节点度数为2）
节点势计算公式如下（其中减号是加号，显示错误）

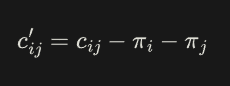
其中π i是节点势
初始势值一般为0
1.对每条边，计算调整后的权重
2.构造1-tree
3.调整节点势

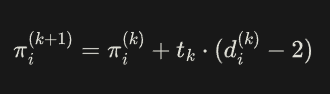
其中d是度数，入为学习率
重复上面三步直到满足足够迭代次数或收敛精度
Step3.计算边的α值

其中α值是在Herd-karp计算中辅助生成的
较小的α值表现该边更可能属于最优解
Step4.基于α值进候选边筛选
根据一个点所连接的不同边的α值，选取最小的5-20条边，加入候选边集
其中实验表明5-20条边即可覆盖几乎所有的最优解边