K-opt算法的结合

在阅读此文章前，默认您已了解k-opt的原理，此处提供一篇文章，不再赘述
Opt算法：2-opt，3-opt，Or-opt，k-opt
简单来说，k-opt就是将城市间的路径移除k条，并对已移除路线的城市进行路径的重新连接，如果总路线距离缩短，则保留总路线
并且它会计算在一定条件下城市间路线的所有可能的连接方式
这使得它的计算量很大

贴个解析(真不是我懒)

所以如果k很大，所选中的城市多了，计算成本会呈指数式增长
而且根据描述不难看出，k-opt只能优化局部间的路线，并不能优化整体的路线
而LKH采用了非常巧妙的方法，不仅利用了k-opt的优点，还尽量让k-opt的缺点(计算难度大)不可见

LKH的原理

LKH最主要利用了这三个机制:
1.动态调整k
2.候选边集
3.回溯机制

动态调整k

解释

需要找到一个合适的临界值
如果k太小，易陷入局部最优
如果k太大，计算难度急剧增大

步骤

Step1.设定初始k值(一般是2)

Step2.构建交换序列
简单来说，就是将边删除和边生成的操作交替形成一条链

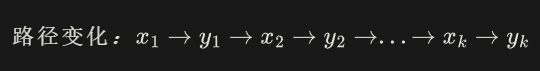
其中x是被删除的边，y是新生成的边

Step3.计算增益
先计算每一步删除边x和生成边y的局部增益

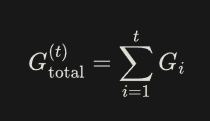
再计算截止至第t步的增益

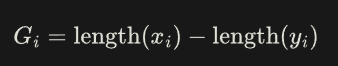
如果G(total)>0，则交换序列有效

Step4.扩展k值
如果G(total+1)仍＞0，则将k值扩展1，并重复操作直到:
1.没有找到任何G>0的情况
2.达到设置的k值限制（无限增长会严重增加计算负担）

Step5.接受最优解
选择G(total)最大的一个解进行交换执行

回溯机制

解释

在迷宫中，当你走入了一个死胡同，你就会回到上一个岔路口，尝试另一条没有走过的路
这就是回溯机制
在上面我们提到，LKH算法会保存交换序列，累计增益等信息
而这些信息都以栈的形式保存
这使得回溯极为便捷

步骤

Step1.判断
当发生以下情况时，会触发回溯:
1.G(total)≤0
2.回溯深度限制就是你回溯太多次了赶紧滚回去别回溯了

Step2.回溯
1.弹出栈顶(因为所有数据以栈方式保存，只要弹出就能使新操作数据消失，即实现回溯)
2.尝试备选边(之前提到过，G(total)的判断只是对单一序列的，其他序列的可能性仍存)
3.继续生成交换序列进行判断
4.如果有更优增益的新路径，则继续，否则回溯

但是回溯之后又可能会遍历所有可能来找到更优增益这计算负担不爆炸了吗
这又要介绍回溯的一个机制:
利用有限深度搜索+剪枝的方式逼近最优解
有限深度搜索:限制深度d
剪枝:采用阈值剪枝，若当前路径G(total)+预估剩余最大增益≤当前已知最优增益，则放弃该路径
预估剩余增益:基于候选边(α-nearness)值计算后续可能的最大增益
该值反映边的重要性(后面会讲)

并且回溯机制包含动态规划记忆的思想，它会记录已探索子路径的最大增益，从而避免重复计算